두 개의 점과 점 사이의 거리 구하기 > 파이썬 팁

점과 점 사이의 거리 구하기

 

프로그래밍으로 2D 그래픽을 처리하려면 반드시 좌표(coordinates)에 대해서 알아야 한다.

 

일반적으로 좌표는 평면을 상하, 좌우로 선을 긋고 좌우의 선을 X축, 상하의 선을 Y축이라 표현한다.

 

X축과 Y축이 만나는 지점을 0으로 두고, 좌표는 (X축의 0점과의 거리, Y축의 0점과의 거리)로 표현된다.

 

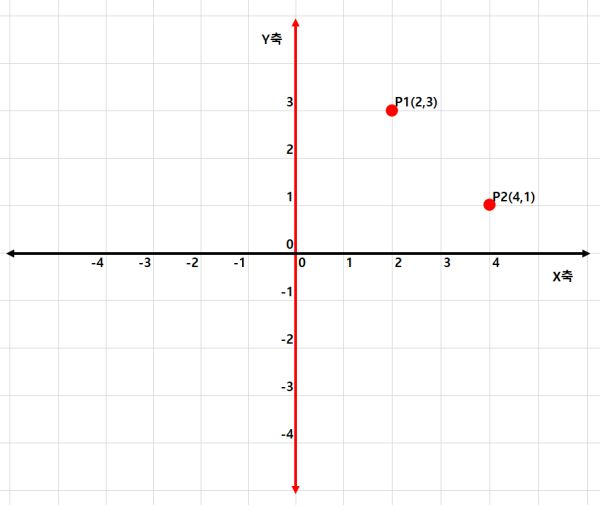
X, Y 축 좌표

 

 

 

위의 좌표 상의 점 P1은 X축으로 2, Y축으로 3인 위치에 존재한다. 또한 P2는 X축으로 4, Y축으로 1인 위치에 존재한다.

 

 

두 점 사이의 거리를 구해보자.

 

우선, 피타고라스의 정리에서 직각을 끼고 있는 변 A, B와 빗변 C와의 관계는 A ** 2 + B ** 2 = C ** 2 와 같다.

 

즉, A의 제곱 + B의 제곱 = C의 제곱이 된다. 

 

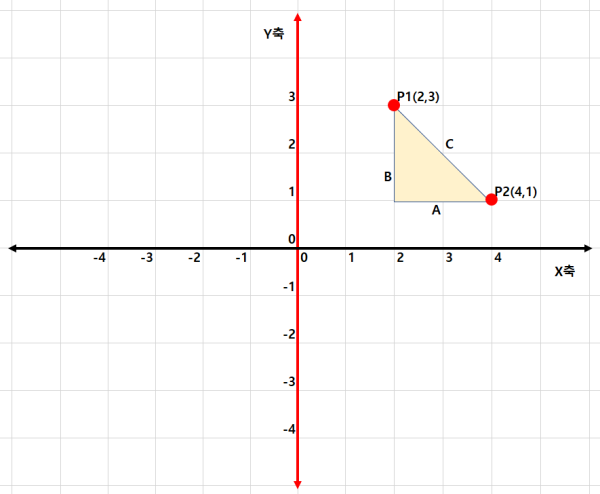
이를 위의 좌표에서 살펴보면 아래와 같다.

 

 

 

위의 그림에서 A의 길이는 2, B의 길이는 2이다.

 

이를 수식으로 표현하면 아래와 같다.

 

A = P2.X - P1.X  = 4 - 2

B = P2.Y - P1.Y = 1 - 3

 

피타고라스의 정리에 의해 A와 B는 제곱을 할 것이므로 P1과 P2의 순서는 관계없다. 즉, P1 - P2 건 P2 - P1이건 상관 없다.

 

파이썬에서 제곱을 만드는 방법은 두가지가 있다. 

 

1. 연산자로 제곱을 만드는 방법

 

    A = P.X ** 2

 

2. 함수로 제곱을 만드는 방법

 

    A = math.pow(P.X , 2)

 

위의 함수를 이용하여 A의 제곱 + B의 제곱을 구하면 아래와 같다.

 

math.pow(P1.X - P2.X , 2) + math.pow(P1.Y - P2.Y , 2)

 

이제 C값을 구하면 된다.

 

하지만 C의 제곱이 A의 제곱 + B의 제곱이므로, 우리가 원하는 점과 점사이의 거리는 A의 제곱 + B의 제곱한 결과의 제곱근(root)을 구해야 한다.

 

파이썬에서 root를 구하는 함수는 math.sqrt이다.

 

따라서 C는 아래와 같이 구할 수 있다.

 

C = math.sqrt( math.pow(P1.X - P2.X , 2) + math.pow(P1.Y - P2.Y , 2) )

 

모든 프로그래밍 공식은 만들어 졌다.

 

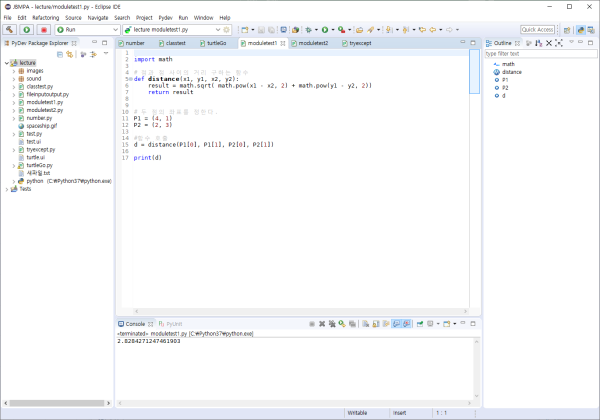
아래의 코드를 통해 실제 적용되는 점과 점 사이의 거리를 구해보자.

 

import math   # 점과 점 사이의 거리 구하는 함수 def distance(x1, y1, x2, y2):     result = math.sqrt( math.pow(x1 - x2, 2) + math.pow(y1 - y2, 2))     return result # 두 점의 좌표를 정한다. P1 = (4, 1) P2 = (2, 3)   #함수 호출 d = distance(P1[0], P1[1], P2[0], P2[1]) print(d)

2.8284271247461903

 

 

 

 

 

점과 점사이의 거리를 2차원 평면상에서 두 개의 객체의 거리라 생각할 수 있다. 따라서 이는 객체 사이의 거리를 계산하는 매우 중요한 방법 중 하나이다. 

 

차후에 간단한 게임을 만들면서 이를 실제 이용해 보도록 한다.